1 Introduction

Voltage Source Converter (VSC) based High Voltage Direct Current (HVDC) grids are expected to play an important role in the development of the future European power system, especially in interconnecting large-scale offshore wind farms and facilitating an integrated European energy market [1]. DC protection system is the one of the key factors in order to build a reliable HVDC grid. Compared to the conventional AC protection system, the DC protection system has particular challenges because of the high rate of rise of the fault current, which results in very stringent time constraints on the DC protection system. In meshed HVDC grids, the total time for the entire fault clearing process using selective protection strategy is considered in the order of several milliseconds which is one order of magnitude below the operating time of AC protection systems [2].

In order to achieve fast and selective protection in HVDC grids, HVDC circuit breakers and selective fault detection relays are necessary. Although HVDC circuit breakers are not commercially available yet, the development of several HVDC circuit breaker prototypes indicates that interrupting DC currents in the order of kA can be achieved in just few milliseconds [3,4,5]. In the literature, most research on DC protection has focused on developing fast and selective DC protection algorithms, which can be categorized into unit protection [6, 7] and non-unit protection [8,9,10,11,12]. Current differential and travelling wave differential algorithms are proposed in [6, 7], respectively, where the first travelling waves are used to distinguish the faulted cable. Non-unit protection algorithms use series inductors at the line terminals to define protection zones, and essentially identify the fault by using information contained in the first voltage/current waves. Due to the reflection by the series inductor at the cable terminal, the first voltage waves at the faulted terminals have distinctive waveforms compared to those at the healthy terminals, and can thus be used for fault discrimination. Although the input signals and discrimination methods of these protection algorithms are different, all algorithms essentially use fault initiated travelling waves to discriminate the faulted line. Therefore, in-depth understanding of the travelling wave behaviour is essential for designing robust DC protection algorithms.

Most proposed protection algorithms, however, have been designed based on extensive time domain simulations for one configuration or test system. Therefore, general applicability or adaptability to different configurations and system changes is not by default ensured. Moreover it is difficult to gain in-depth understanding of the influencing parameters through time domain simulations. Additionally, the future HVDC grids can be developed into monopolar, bipolar, or more complex configurations, such as a bipolar backbone with monopolar tappings [13,14,15]. Such a complex future system might have various grounding schemes, such as low impedance grounding or ungrounded stations. The grounding points and the number of parallel branches connected to a busbar in a meshed HVDC grid may change due to system reconfiguration, maintenance, or outage. Furthermore, the inductors in series with the DC circuit breakers fundamentally influence the travelling wave behaviour, and the size of these inductors might take various values depending on the requirements from the DC circuit breakers [3, 4] and DC grids [16]. However, protection settings are preferred to be insensitive to changes in the system conditions. Therefore, the influence of these changes on the travelling wave behaviour needs to be studied properly. A Laplace domain-based grid modelling [9] allows to systematically study such effects. This paper builds on this travelling wave-based approach to study fault behaviour in bipolar, asymmetrical and symmetrical monopolar systems. In doing so, the paper provides the guidelines needed for the design of multivendor protection algorithms.

The paper is arranged as follows. First, voltage and current wave transfer functions with respect to the incident voltage wave are derived for meshed bipolar HVDC grids. Second, the frequency domain based model is validated against time domain simulation using a detailed model implemented in PSCAD™. Third, the induced voltages and currents by the incident voltage wave on the positive and negative poles are analysed in order to understand the degree of the mutual coupling between the two poles. Fourth, the influences of system changes such as number of parallel branches, grounding impedances and series inductors on the travelling waves are analysed for a bipolar HVDC grid. Finally, the influences of different HVDC configurations and grounding schemes are investigated.

2 Travelling waves in bipolar HVDC grids

In meshed HVDC grids, the DC fault clearing should typically be achieved in the order of few milliseconds; therefore, selective fault detection and discrimination typically has to be achieved within 1 ms after the fault reaching the relay [9,10,11]. During this time frame, the fault behaviour is dominated by the travelling wave phenomenon. For long cable lengths, reflected waves at the remote stations are outside the time frame of interest (e.g. cable length \({>}75\) km) and the analysis can be limited only to the first reflection of the incident wave [9]. For DC faults along the cable, the first voltage wave front contains the most important information for fault detection and discrimination. This paper therefore only focuses on the analysis of the first reflection and transmission of the incident wave arriving at a converter station.

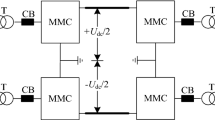
The converter station under study can be expressed as shown in Fig. 1, where the measurement relays are placed between the cable terminals and the series inductors. The voltages and currents at the relay positions are typically used for fault identification and are thus of interest for the analysis. \(e_{i}\) is the incident voltage wave arriving at the relay position of the faulted cable, and \(e_{r}\) is the reflected voltage wave at this point. The resulting voltage and current are \((e_{0}, i_{0})\). The voltage and current transmitted to the adjacent cables in the positive pole and to the cables in the negative pole are denoted as \((e_{pk}, i_{pk})\) and \((e_{nk}, i_{nk})\), respectively. The number of cables connected to the positive, neutral and negative polarity terminals of the converters are \(N_{p},N_{m}\) and \(N_{n}\), respectively. The number of cables in each pole can be different considering maintenance, outage, or an asymmetric configuration. The characteristic impedance of the cables are denoted as \(Z_{Cp1}(s)\), …, \(Z_{CpNp}(s)\), \(Z_{Cm1}(s)\), …, \(Z_{CmNm}(s)\) and \(Z_{Cn1}(s)\), …, \(Z_{CnNn}(s)\), respectively. \(L_{p1}\), …, \(L_{pNp}\) and \(L_{n1}\), …, \(L_{nNn}\) are the series inductors of the DC circuit breakers in the positive and negative poles. \(Z_{conv}(s)\) is the equivalent impedance of the converters. The grounding impedance is represented by \(Z_{g}(s)\), which could be infinite if the converter station is ungrounded, resistive, inductive or zero depending on the grounding scheme.

Fig. 1
figure 1

Travelling waves at a bipolar converter station with a fault at point F

Full size image

2.1 Travelling wave transfer functions

The surge impedance of each portion, looking from the position of the measurement relay at the faulted cable, is denoted in Fig. 1 for the purpose of deriving travelling wave transfer functions. The surge impedances of the parallel branches of the positive (excluding the faulted cable), neutral and negative poles, \(Z_{p}(s),Z_{m}(s)\) and \(Z_{n}(s)\), are

$$\begin{aligned} \left\{ \begin{aligned}&Z_{p}(s) =(sL_{p2}+Z_{Cp2}(s))//\dots //(sL_{pNp}+Z_{CpNp}(s))\\&Z_{m}(s) =Z_{Cm1}(s)//\dots //Z_{CmNm}(s)\\&Z_{n}(s) =(sL_{n1}+Z_{Cn1}(s))//\dots //(sL_{nNn}+Z_{CnNn}(s))\\ \end{aligned} \right. \end{aligned}$$
(1)

Using basic circuit theory, the surge impedances of the noted four portions in Fig. 1 \(Z_{j}(s), \,{\text{j}}=1, 2, \dots ,4\) are

$$\begin{aligned} \left\{ \begin{aligned}&Z_{1}(s) = Z_{p}(s)//Z_{2}(s)\\&Z_{2}(s) = Z_{conv}(s) + Z_{3}(s)\\&Z_{3}(s) = Z_{m}(s)//Z_{g}(s) //Z_{4}(s)\\&Z_{4}(s) = Z_{conv}(s) + Z_{n}(s) \end{aligned} \right. \end{aligned}$$
(2)

Then, the total surge impedance seen by the faulted cable at its terminal, \(Z_{0}(s)\) is

$$\begin{aligned} Z_{0}(s) = sL_{p1}+ Z_{1}(s) \end{aligned}$$
(3)

The resulting voltage and current \((e_{0}(s),i_{0}(s))\) at the relay position are now a function of the incident voltage wave

$$\begin{aligned} \left\{ \begin{aligned} e_{0}(s)&= \frac{2Z_{0}(s)}{Z_{0}(s)+Z_{Cp1}(s)}\cdot e_{i}(s)\\ i_{0}(s)&= \frac{2}{Z_{0}(s)+Z_{Cp1}(s)}\cdot e_{i}(s)\\ \end{aligned} \right. \end{aligned}$$
(4)

and the voltage and current transmitted to the adjacent cables \((e_{pk}(s),i_{pk}(s))\) are given by

$$\begin{aligned} \left\{ \begin{aligned} e_{pk}(s)&= \frac{Z_{Cpk}(s)}{sL_{pk}+Z_{Cpk}(s)}\cdot Z_{1}(s)\cdot i_{0}(s)\\ i_{pk}(s)&= \frac{e_{pk}(s)}{Z_{Cpk}(s)},\quad k = 2,3\dots , N_{P}\\ \end{aligned} \right. \end{aligned}$$
(5)

Similarly, the voltage and current transmitted to the cables in the negative pole \((e_{nk}(s),i_{nk}(s))\) are given by

$$\begin{aligned} \left\{ \begin{aligned} e_{nk}(s)&= \frac{Z_{Cnk}(s)}{sL_{nk}+Z_{Cnk}(s)}\cdot \frac{Z_{n}(s)}{Z_{4}(s)}\cdot \frac{Z_{3}(s)}{Z_{2}(s)}\cdot Z_{1}(s)\cdot i_{0}(s)\\ i_{nk}(s)&= \frac{e_{nk}(s)}{Z_{Cnk}(s)},\quad k = 1,2\dots , N_{n}\\ \end{aligned} \right. \end{aligned}$$
(6)

The voltage and current transfer functions are defined with respect to the incident voltage wave \(e_{i}(s)\) as

$$\begin{aligned} \left\{\begin{aligned} G_{j}(s) = \frac{e_{j}(s)}{e_{i}(s)}\\H_{j}(s) = \frac{i_{j}(s)}{e_{i}(s)} \end{aligned} \right. \end{aligned}$$
(7)

where \(j= \{0, pk, nk\}\) for the faulted cable, adjacent cables of the positive pole and cables of the negative pole, respectively.

The voltage and current transfer functions can be obtained by dividing (4), (5) and (6) by \(e_{i}(s)\). For the faulted cable terminal,

$$\begin{aligned} \left\{ \begin{aligned} G_{0}(s)&=\frac{2Z_{0}(s)}{Z_{0}(s)+Z_{Cp1}(s)}\\ H_{0}(s)&= G_{0}(s)/Z_{0}(s)\\ \end{aligned} \right. \end{aligned}$$
(8)

and for the adjacent cables in the positive pole,

$$\begin{aligned} \left\{ \begin{aligned} G_{pk}(s)&= \frac{2Z_{Cpk}(s) Z_{1}(s)}{(sL_{pk}+Z_{Cpk}(s)) (Z_{0}(s)+Z_{Cp1}(s))} \\ H_{pk}(s)&= G_{pk}(s)/Z_{Cpk}(s) \\ \end{aligned} \right. \end{aligned}$$
(9)

where \(k=2,3\dots , N_{p}\).

Similarly, the voltage and current transfer functions for the cables in the negative pole are given by

$$\begin{aligned} \left\{ \begin{aligned}&G_{nk}(s) = \frac{2Z_{Cnk}(s) Z_{n}(s) Z_{3}(s)Z_{1}(s)}{(sL_{nk}+Z_{Cnk}(s))Z_{4}(s)Z_{2}(s)(Z_{0}(s)+Z_{Cp1}(s))}\\&H_{nk}(s) = G_{nk}(s)/Z_{Cnk}(s)\\ \end{aligned} \right. \end{aligned}$$
(10)

where \(k=1,2\dots , N_{n}\).

2.2 Frequency domain component models

This section describes the frequency domain models of the components used in this paper.

2.2.1 Cable characteristic impedance

Distributed parameter frequency dependant models of transmission lines are used to describe the voltage and current travelling waves along transmission lines. In such a representation, a transmission line is characterized by two matrix transfer functions: the propagation matrix \(\varvec{H}\) and the characteristic impedance matrix \(\varvec{Z}_{C}(s)\). The frequency dependency of these matrices can be approximated using rational functions in the frequency domain [17].

$$\begin{aligned} f(s) = d + s\cdot h+ \sum ^N_{i=1}\frac{c_{i}}{s-a_{i}} \end{aligned}$$
(11)

where, \(c_{i}\) are the residues, \(a_{i}\) are the poles, d, h are real constants, and N is the approximation order.

In this paper, the parameters for the cable geometry and materials are taken from [18]. The parameters in (11) are obtained via the PSCAD™ Line Constants Program [19]. Only the diagonal elements of the characteristic impedance and propagation matrices are used in the study considering that mutual impedances between cables are relatively small [20]. All the cables are assumed to have the same characteristic impedance in this paper. Note that in practical systems, the conductor and the insulating layer of the metallic return cables can have smaller diameters compared to those of the main cables due to lower requirements on the return cables.

2.2.2 Equivalent impedance of MMC converters

The converter topology considered in this study is half-bridge based modular multilevel converter (HB-MMC). The behaviour of a HB-MMC during a DC fault can be divided into capacitive discharge stage and diode rectifier stage starting after blocking the Insulated Gate Bipolar Transistors (IGBTs) [21]. In the first milliseconds after a DC fault before blocking the IGBTs, only the capacitive discharge stage needs to be taken into account. The HB-MMC converter is modelled by an equivalent RLC circuit in line with the model from [21]. The capacitive discharge of the submodules is approximated by an equivalent capacitance which is equal to the total capacitance of the inserted submodules prior to the arrival of the fault wave.

$$\begin{aligned} Z_{conv}(s) = sL_{eq} + R_{eq} + \frac{1}{sC_{eq}} \end{aligned}$$
(12)

where \(L_{eq}, R_{eq}\) and \(C_{eq}\) are the equivalent inductance, resistance and capacitance.

In order to validate the RLC representation of the MMC converter, a comparison between the frequency response of the RLC equivalent model and the simulated impedance responses is given in Fig. 2. Main parameters of the converter model, taken from [22] are given in Table 1. The simulated impedance response are calculated using frequency sweeping on a continuous MMC model implemented in PSCAD™ [18]. Figure 2 shows that first, the operating point of the converter influences the converter impedance in the low frequency region. Second, the RLC equivalent model matches with the simulated impedances in the high frequency region very well. Since the time range concerned in this study is only the first millisecond, the RLC model is considered to have sufficient accuracy.

Fig. 2
figure 2

Comparison of the equivalent impedance of the MMC converter between the RLC model and frequency-sweep in PSCAD™

Full size image
Table 1 Converter parameters (rating: 500 MVA)
Full size table

3 Evaluation against PSCAD™ models

In this section, the frequency domain model is validated by comparing the step response of the transfer function with time domain simulations based on detailed models implemented in PSCAD™. A four terminal bipolar test system in Fig. 3 adapted from the symmetric monopolar grid [18] is used to perform the comparison. Main parameters of the test system are given in Table 2. Mutually coupled distributed parameter frequency dependent cable models are used in the simulation. The cable parameters and configurations are given in Table A1 and Fig. A1 in the “Appendix A”. Both pole-to-ground and pole-to-pole fault at 8 fault locations along cable L13 are simulated. Two values of the series line inductors 50 mH and 100 mH are used.

Fig. 3
figure 3

A four terminal bipolar test system used in PSCAD™ simulations

Full size image
Table 2 Grid parameters and simulation conditions
Full size table

Figure 4 shows the calculated and simulated voltages \(e_{0}(t)\) at the cable terminal for pole-to-ground faults applied at 25, 100 and 200 km from Bus 1. It is shown that the calculated response corresponds well with the simulated waveforms for the first reflection. This validates that neglecting mutual coupling of the cables in the transfer function is acceptable. The difference between the calculated and the simulated response using a detailed converter model diverges more for a longer period of time. This difference is due to the fact that the RLC representation of a converter is mainly accurate in the high frequency region. The evaluation window of the maximum difference is taken as the time window of the first reflection up to 1 ms. As shown in Fig. 5, the maximum difference is larger for remote faults, mainly because the evaluation window is longer for remote faults. Nevertheless, the maximum difference within the first reflection is 0.038 p.u. at 320 kV base, which verifies that frequency domain based transfer function provides a valid representation for the first travelling wave behaviour with good accuracy.

Fig. 4
figure 4

Comparison between calculated step responses and PSCAD™ simulations  (F1, F4 and F8 are cable L13 faults located 25, 100 and 200 km from Bus 1; Cal are calculated from transfer function; Sim are simulation results from PSCAD™)

Full size image
Fig. 5
figure 5

Maximum differences between calculated step responses and PSCAD™ simulations (ptg: pole-to-ground faults, ptp: pole-to-pole faults)

Full size image

4 Mutual coupling in bipolar HVDC links

In a bipolar configuration, it is important to understand to what extent the fault behaviour in one pole influences the other pole. In this study, frequency and step responses of the voltage and current transfer functions are used to investigate the mutual coupling of the two poles.

The bode magnitude plots of the voltage and current transfer functions in (8) and (10) are shown in Fig. 6 assuming a point-to-point bipolar link (\(N_{p},\; N_{m},\; and\; N_{n}=1\)). The converter station is assumed to be ungrounded considering that if the converter station is low-impedance or solidly grounded, the influence on the negative pole is insignificant or non-existent. Figure 6 gives the bode plots of the transfer functions in absolute magnitude. Figure 7 gives the step responses of the transfer functions up to 1 ms. Since a DC fault initiated incident voltage wave approximates a step change, the step responses of the transfer functions are corresponding to time domain simulations of DC faults at the cable terminal.

Fig. 6
figure 6

Frequency responses of voltage and current transfer functions (color indicates transfer functions while line styles—solid, dotted, densely dashed, dashdotted and loosely dashed—indicate the size of the inductor)

Full size image

Figure 6a shows that \(G_{0}(s)\), the transfer function of the resulting voltage at the faulted cable, has the characteristic of a band-rejection filter. The gain of the high frequency region for all series inductor values is approximately 2, which means the high-frequency components of the incident wave are doubled, i.e. totally reflected at the faulted cable terminal. The resonant frequency of this equivalent band-rejection filter is largely determined by the series resonance of the equivalent converter capacitance \(C_{eq}\) and by the sum of the equivalent converter inductance and the series inductor \(L_{eq}+L_{p1}\). A large series inductor shifts the resonant frequency to lower frequencies. Besides, it also reduces the bandwidth of the rejection range, which results in reflecting more low frequency components. As shown in Fig. 6a, the upper cut-off frequency shifts from approximately \(10^4\) Hz to \(10^2\) Hz when the series inductor increases from 0 mH to 300 mH. Figure 7a shows the step responses of \(G_{0}(s)\), which have a initial magnitude of 2 corresponding to total reflection of the high frequency components. The step response of \(G_{0}(s)\) with a small series inductor decays much faster as more frequency components are located in the bandwidth of the rejection range.

As shown in Fig. 6b, \(H_{0}(s)\), the resulting current transfer function at the faulted cable terminal, has the characteristic of a band-pass filter. Since \(H_{0}(s)\) is defined with respect to the incident voltage wave, it can be considered as an admittance which describes the relationship between the resulting current at the faulted cable terminal and the incident voltage. This admittance is highly inductive due to the presence of the series inductor and the converter arm inductors. Consequently, high-frequency components of the incident voltage are largely attenuated. In the low frequency region, this admittance is highly capacitive, mainly due to the equivalent converter capacitor. As a result, low-frequency components of the incident voltage are also largely attenuated. The bandwidth and gain of the frequency response of \(H_{0}(s)\) increase as the series inductors decrease.

\(G_{nk}(s)\) and \(H_{nk}(s)\), the voltage and current transfer functions at the negative pole, also have characteristics of band-pass filters, as shown in Fig. 6a, b. The high-frequency components of the incident wave are well damped, and the larger the series inductor, the smaller the bandwidth becomes. Moreover, even without the series inductor, high-frequency components still can not pass to the negative pole because the inductive behaviour of the converter. This can also be confirmed by the step responses of \(G_{nk}(s)\) and \(H_{nk}(s)\) in Fig. 7, which have much smaller amplitudes compared to those of \(G_{0}(s)\) and \(H_{0}(s)\). Therefore, in terms of very fast transients in the first millisecond, the mutual coupling between the two poles of a cable-based bipolar system is found to be insignificant.

5 Influences of system changes on travelling waves in meshed bipolar HVDC grids

This section analyses the influence of system changes on the travelling waves in meshed bipolar HVDC grids. The considered parameters are the number of the parallel branches in the positive pole, the grounding impedance and the series inductor value.

5.1 Number of parallel branches

The number of the branches in the positive pole \(N_p\) is varied from 1 to 4, while the total numbers of the parallel branches in the neutral and negative poles, \(N_m\) and \(N_n\) are fixed at 4. The frequency and step responses of \(G_{0}(s)\) and \(G_{pk}(s)\) are shown in Figs. 8 and 9 respectively for different number of parallel branches \(N_p\) and different values of the series inductors L.

Fig. 7
figure 7

Step responses of voltage and current transfer functions (color indicates step responses while line styles—solid, dotted, densely dashed, dashdotted and loosely dashed—indicate the size of the inductor)

Full size image
Fig. 8
figure 8

Influence of number of parallel branches: frequency responses of voltage transfer functions (color indicates the number of parallel branches while line styles—solid, dotted, dashed and dashdotted—indicate the size of the inductor)

Full size image

Figure 8a, b shows that if the series inductor is zero, the voltages at the faulted and healthy cables are exactly the same since the cables are connected to the same electrical point. The gain of \(G_{0}(s)\) and \(G_{pk}(s)\) in the low and high frequency regions is approximately equal to \(\frac{2}{N_p}\), with \(N_p>2\) considering \(Z_{conv}(s) \gg Z_C(s)\) in both the low and high frequency region.

As shown in Fig. 8b, \(G_{pk}(s)\), the voltage transfer function of the adjacent cables has a more complex behaviour in the case that series inductors are present. The size of the series inductor changes both the shape and the cut-off frequency, beyond which \(G_{pk}(s)\) has a gain close to 0. Furthermore, large series inductors reduce the cut-off frequency of the frequency responses. The influence of the number of the parallel branches is more pronounced in the low-frequency region, where the cable characteristic impedance is more dominant compared to the influence of the series inductors. The step responses in Fig. 9b also give an indication of the margins, in terms of both time and voltage level, to discriminate the faulted cable from the adjacent ones. For instance, as shown in Fig. 9a, b fault discrimination will only have about 0.2 ms for a series inductor of 10 mH if voltage level is used for discrimination, whereas large inductors allow more time and larger margins to discriminate the faulted cable.

Fig. 9
figure 9

Influence of number of parallel branches: step responses of voltage transfer functions (color indicates the number of parallel branches while line styles—solid, dotted, dashed and dashdotted—indicate the size of the inductor)

Full size image

5.2 Grounding impedance

Bipolar HVDC systems are typically solidly or low-impedance grounded and it can be expected such groundings also in VSC-HVDC [13]. However, a converter station can be grounded or ungrounded depending on the operation conditions. The grounding options considered in this section are solid grounding (\(Z_{g}(s)=0\,\Omega\)), resistance grounding (\(Z_{g}(s)=10\,\Omega\)), inductance grounding of 50 mH (\(Z_{g}(s)=0.05\,s\)) and ungrounded (\(Z_{g}(s)=\infty\)). The total number of the parallel branches in all three layers, \(N_p,N_m\) and \(N_n\) is chosen equal to 3.

Figures 10 and 11 show the frequency and step responses of \(G_{0}(s)\) for different grounding impedances and series inductances. It can be seen that the grounding impedance has an insignificant influence on the frequency response and only modifies the frequency response near the resonant frequency region, which corresponds to the series LC resonance of the converter. In both low and high-frequency region, the large impedance of the converter blocks the influence of any changes in the neutral and negative pole. The step responses shown in Fig. 11 confirms the analysis in the frequency-domain.

Fig. 10
figure 10

Influence of grounding scheme: frequency responses of the voltage transfer function \(G_{0}(s)\) (color indicates grounding impedances while line styles—solid, dotted, dashed and dashdotted—indicate the size of the inductor)

Full size image
Fig. 11
figure 11

Influence of grounding scheme: step responses of the voltage transfer function \(G_{0}(s)\) (color indicates grounding impedances while line styles—solid, dotted, dashed and dashdotted—indicate the size of the inductor)

Full size image

6 Influences of HVDC configurations with different grounding schemes

As future HVDC grids can have more complex configurations with mixed bipolar and monopolar configurations, the influences of HVDC configurations with different grounding schemes on the travelling wave are investigated in this section. The impact of HVDC configurations with different groundings is evaluated by comparing the voltage transfer functions with that of a solidly grounded bipolar configuration.

Figure 12 shows the asymmetrical and symmetrical monopolar configurations for a converter station. The voltage transfer functions at the faulted cable terminal have the same form as (8), while the total surge impedance seen by the faulted cable are \(Z^{Asym}_{0}(s)\) and \(Z^{Sym}_{0}(s)\).

$$\begin{aligned} \left\{ \begin{aligned}&Z^{Asym}_{0}(s) = sL_{p1}+Z_{p}(s)//\left[ Z_{conv}(s) + Z^{Asym}_{3}(s)\right] \\&Z^{Sym}_{0}(s) = sL_{p1}+Z_{p}(s)//\left[ Z_{conv}(s) + Z^{Sym}_{3}(s)\right] \\ \end{aligned} \right. \end{aligned}$$
(13)

Obviously, only the equivalent impedance of the neutral and negative poles, denoted as \(Z_{3}(s)\), differs depending on HVDC system configurations and their grounding schemes. As shown in (13), \(Z_{3}(s)\) is in series with the converter surge impedance \(Z_{conv}(s)\); therefore, a comparison between \(Z_{conv}(s)\) and \(Z_{3}(s)\) is performed to analyse the impact of HVDC configurations with different groundings. The number of the parallel branches and the series inductors are chosen equal to 3 and 50 mH, respectively. The grounding impedances are set the same as in Sect. 5.2, respectively.

A summary of \(Z_{3}(s)\) for different configurations and groundings is given in Table 3. It is obvious that the total surge impedances are the same for solidly grounded asymmetrical monopolar and bipolar configurations regardless of return paths. Therefore, the voltage/current transfer functions are the same in these configurations. Figure 13 shows that the configurations can largely be divided into two groups, the first group (\(\hbox {Grp}_{\mathrm{I}}\)), where \(Z_{3}(s)\) is negligible compared to \(Z_{conv}(s)\) in the high frequency region (\(f >10^2\) Hz) and the second group (\(\hbox {Grp}_{\mathrm{II}}\)), where \(Z_{3}(s)\) is comparable to \(Z_{conv}(s)\) in the high frequency region.

Table 3 \(Z_{3}(s)\) for different configurations and groundings
Full size table

The differences of the step responses between each configuration and the solidly grounded bipolar configuration are defined by

$$\begin{aligned} {\Delta } g(t) ={\mathcal {L}}^{-1} \left\{ \frac{G_{0,x}(s)-G_{0,grded}(s)}{s}\right\} \end{aligned}$$
(14)

where x represents configurations listed in Table 3.

For asymmetrical and symmetrical monopolar configurations, two converter dimensions are considered in the comparison. One is the same dimension as the bipolar configuration, 500 MVA per converter, for the purpose of comparing the influence of HVDC configurations and grounding. The other is 900 MVA in Table 4, which is more realistic sizing of existing offshore links.

Table 4 Converter parameters (rating: 900 MVA [18])
Full size table

Frequency responses of \(G_{0}(s)\) under different configurations and groundings are shown in Fig. 14. The symbols used to represent the configurations in Fig. 14 are listed in Table 3. Figure 15 shows \({\Delta } g(t)\), the differences of the step responses between each configuration and the solidly grounded bipolar configuration with converter dimension rated at 500 MVA. As shown in Fig. 15a, for the same converter dimension, these differences of \(\hbox {Grp}_{\mathrm{II}}\) cannot be neglected, especially for small series inductors. On the contrary, the differences of \(\hbox {Grp}_{\mathrm{I}}\) are less than 0.2 % up to 0.2 ms, even with series inductors of 10 mH. In the cases using a 900 MVA converter, the differences of both groups with respect to the reference case are slightly larger than those of the cases with the same converter size. In terms of fast transients, \(\hbox {Grp}_{\mathrm{I}}\) and \(\hbox {Grp}_{\mathrm{II}}\) can be considered as effectively low and high impedance grounded, respectively. The behaviour of the travelling waves of \(\hbox {Grp}_{\mathrm{I}}\) is comparable to that of a solidly grounded bipolar configuration, while the fast transient behaviour of \(\hbox {Grp}_{\mathrm{II}}\) is only comparable to that of a solidly grounded bipolar configuration when the series inductors are large.

Fig. 12
figure 12

Travelling waves at a converter station

Full size image
Fig. 13
figure 13

Comparison between \(Z_{conv}(s)\) and \(Z_{3}(s)\) of different configurations, \(L=50\) mH

Full size image
Fig. 14
figure 14

Influence of configuration and grounding: frequency responses of voltage transfer functions \(G_{0}(s)\), \(N_p,N_m\), and \(N_n=3\) (color indicates HVDC configuration and grounding schemes while line styles—solid, and dashdotted—indicate the size of the inductor)

Full size image
Fig. 15
figure 15

Influence of configuration and grounding: step response differences compared to solidly grounded asymmetric monopolar/bipolar system with 500 MVA converter \({\Delta } g(t)\), \(N_p,N_m\), and \(N_n=3\) (color indicates HVDC configuration and grounding schemes while line styles—solid, and dashdotted—indicate the size of the inductor)

Full size image

7 Conclusion

In this paper, a frequency-domain based methodology to analyse the travelling wave behaviour in meshed HVDC grids has been proposed. A comparison of the step response calculated using transfer function and time domain simulation using a detailed model in PSCAD™ verified that frequency domain based transfer function provides a valid representation for the first travelling wave behaviour with good accuracy. By analysing the frequency responses of the voltage/current transfer functions with respect to the incident voltage wave, the influences of the system parameters on the first travelling waves can be accurately predicted without the need for performing extensive time domain simulations.

The proposed methodology is used to analyse the travelling waves in a bipolar configuration with metallic return. First, the mutual coupling, in terms of very fast transient between the two poles is shown to be insignificant. Second, the influence of the number of the parallel branches in the same pole, is shown to be more pronounced in the low-frequency region, which implies that very fast transients are less influenced by the number of the parallel branches. Third, the series inductor at the cable terminal plays vital role in primary protection algorithms based on local measurements. Large series inductors give large margin in both voltage detection level and the time to identify the faulted cable. Fourth, the grounding impedances in a bipolar system have insignificant influences on the first travelling wave.

In addition, the travelling wave behaviours under different HVDC configurations and groundings have been analysed. Among the configurations considered in this study, both asymmetrical monopolar/bipolar configuration with metallic returns regardless of grounding and low resistive-grounded/solidly grounded asymmetrical monopolar/bipolar configuration with ground return are effectively low-impedance grounded in terms of fast transients. Symmetrical monopolar configuration and inductive-grounded asymmetrical monopolar/bipolar configuration with ground return can be considered as effectively high-impedance grounded in terms of fast transients. The behaviour of the first travelling waves is comparable between the configurations within the first group while only comparable to those when the series inductors are large.