1 Introduction

The concern for power quality in electrical systems has always been present but has increased dramatically in the last few years due to the simultaneous increase of polluting loads and sensitive ones. Modern industrial equipment has become the major cause of the degradation of power quality as the currents drawn by these non-linear loads have a high harmonic contents. They distort the voltage at the point of coupling to the utility grid and affect the operation of critical loads [1].

Custom power devices based on voltage source converters (VSCs) have already been proposed to compensate for power quality problems in distribution networks. They can be used for active filtering, load balancing, power factor correction and voltage regulation [2]. They can be implemented as shunt type, series type, or a combination of both. Each topology is appropriate for a different set of load and/or supply problems [3].

When series and shunt active power compensators are combined into a single device they make what is called a unified power quality conditioner (UPQC) [4] which is the low-voltage counterpart of a unified power flow controller (UPFC). UPQCs are applicable when both voltage and current power quality problems have to be compensated for in distribution networks [5, 6]. The series converter of the UPQC compensates for the voltage distortion of the grid to protect sensitive loads while the shunt converter compensates for the current harmonics drawn by disturbing loads in order to obtain a clean grid current. Besides, the shunt converter can supply reactive power and should maintain a constant DC voltage in the device compensating for all losses. So far, the controllers proposed for UPQCs have always relied on a fixed grid frequency but, nowadays, the interest in using the UPQC for microgrids (even in island mode) is also increasing [7, 8] and this scenario will certainly require to tackle power quality issues with grid frequency variations larger than those experimented in classical distribution networks [9, 10]. Consequently, the UPQC must adapt to these frequency changes. Apart from the fixed-grid-frequency approach present in the literature, UPQCs have some other obvious drawbacks:

  1. 1)

    High costs: UPQCs require high switching frequency, \(f_{sw}\) (typically \(f_{sw} \ge 10\) kHz in [4, 5, 11,12,13]) and require a complex hardware (two converters, sensors, passive filters and series transformer). Besides, hysteresis current controllers are often used with variable switching frequency posing a complicated design problem [11].

  2. 2)

    Low reliability: the control of a UPQC requires a large number of sensors, specially when an LCL filter is used for the shunt compensator. Therefore, there are a large number of elements that can fail and make the UPQC uncontrollable.

  3. 3)

    Complexity: simultaneous control of two converters requires complex design and tuning processes [14].

In order to mitigate the above disadvantages, the control of a UPQC has been revisited in this work and several proposals for improvement are presented in this paper. First of all, the control of both, series and shunt compensators, has been split into an inner (or main) and an auxiliary (or harmonic) controller. the former takes care of issues related to the grid-frequency component of the electrical magnitudes such as the flow of active and reactive power while the latter takes care of voltage and current unbalance and harmonic compensation. This hierarchical approach is not new in power electronics control [14]. Secondly, Park’s Transformation has been used to refer all electrical variables of both compensators to a reference frame synchronously rotating with the voltage space vector of the point of common coupling (PCC) (main synchronous rotating frame). In this reference frame, the positive sequence of the grid-frequency components of all electrical variables are DC magnitudes in steady state and linear controllers have been used for the inner loop. Among the many possible alternatives, a linear quadratic regulator (LQR) [15] has been chosen for the main controller because it ensures good stability margins [16] and makes it possible to damp the resonance of the passive filters used for the series and parallel compensators. The design of the LQR for the UPQC converters is more complicated than in [15] where a single-L filter is considered and there is no need to damp any resonance. The advantages of LQR with respect to traditional PI controllers were already highlighted in [14] and they become more apparent as the system complexity grows. Thirdly, a Kalman filter (KF) has been used to reduce the number of sensors required to control the inner loops of the UPQC [17]. The combination of the LQR and the KF is known as linear quadratic Gaussian regulator (LQG) [18].

Fourthly, voltage and current unbalance and harmonics are compensated for by using the multiple synchronous reference frame (SRF)-based controller proposed in [19] for series devices and in [20] for shunt devices. This approach avoids the use of resonant controllers (RCs) like those in [14] but it is proved in [19, 20] that the resulting controller is mathematically equivalent to use of RCs in a stationary reference frame. This harmonic controller ensures zero-error tracking of the harmonic components and gives the UPQC a seamless frequency-adaptation capability during grid frequency variations. This last feature was never addressed before in the literature related to UPQCs. The implementation proposed in [19, 20] is very efficient because only two trigonometric functions are calculated and the results are provided by a phase locked loop (PLL) which synchronises the converters with the grid.

Clearly, the application of a multiple SRF-based controller here is a consequence of the good results found in [19, 20] but the coordination of the series and shunt compensation was not included in those references and will be detailed in this paper. The LQG approach for the design of the inner (or main) controller was not used in those references, either, where arbitrary pole placement was used. Therefore, the present paper will illustrate that it is feasible to save a number of sensors while another tuning procedure for the same state-variable based controller is used. Obviously, there is no reason to believe that the closed-loop poles provided by the LQR algorithm could not be selected by some other procedure.

Finally, the controller-design steps have been simplified and only three parameters have to be chosen for each converter: one for the LQR, one for the KF and another one for the harmonic controller.

The proposed control strategy has been fully tested on a 5 kVA dSpace-based prototype and excellent performance has been recorded during compensation of balanced and unbalanced grid-voltage sags, grid-voltage harmonics and load-current harmonics. All this, even under grid-frequency variations, which is a scenario never addressed before with a UPQC.

2 Modelling considerations for UPQC

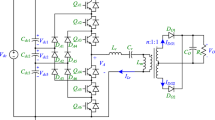
A three-phase UPQC is depicted in Fig. 1. A right-side UPQC is used because in this case the current through the series transformer is almost sinusoidal as the shunt converter compensates for the current harmonics of the load [12]. Besides, the shunt compensator can control the DC voltage regardless the grid voltage value as it is directly connected to the output of the series transformer where voltage harmonics, swells, sags and unbalance should be filtered out. In this scenario, the model of the UPQC can be split in two independent models, one for each compensator [4].

Fig. 1
figure 1

Schematics for a three-phase UPQC

Full size image

2.1 On shunt compensator

The shunt power converter of the UPQC is connected to the PCC through an LCL filter which keeps the switching-frequency ripple of the current (and voltages in weak grids) very low. This helps to avoid high-fequency swiching and current-hysteresis controllers. Table 1 summarizes the value of the parameters used for the shunt compensator in Fig. 1 and the grid characteristics. These parameter values have been used in the prototype and in the theoretical analysis of the paper.

Table 1 Parameters of grid and shunt compensator
Full size table

As the series compensator will inject a controlled voltage in series with the PCC voltage, it can be considered as a voltage disturbance in the shunt compensator model. Accordingly, the state-space model of the shunt compensator after Park’s Transformation is applied takes the form of:

$$\frac{{{\text{d}}\varvec{x}}}{{{\text{d}}t}} = \varvec{Ax} + \varvec{B}_{1} \varvec{u}_{1} - \varvec{B}_{2} \varvec{u}_{2}$$
(1)
$$\varvec{y} = \varvec{Cx} + \varvec{D}_{1} \varvec{u}_{1} + \varvec{D}_{2} \varvec{u}_{2 }$$
(2)

where the vector of state variables is \(\varvec{x} = [i_{Lf1d}\) \(i_{Lf1q}\) \(v_{Cf2d}\) \(v_{Cf2q} i_{Lf2d}\) \(i_{Lf2q} ]^{t}\); the input vector is \(\varvec{u}_{1} = [v_{id} ,v_{iq} ]^{t}\); \(\varvec{u}_{2} = [v_{pccd} + u_{Cfd} ,v_{pccq} + u_{Cfq} ]^{t}\) is the disturbance vector and the output vector (to be controlled) is \(\varvec{y} = \left[ {i_{Lf2d}\,\, i_{Lf2q} } \right]\); A, B 1, B 2, C, D 1, D 2 can be obtained analysing the circuit in Fig. 1 and can be found in detail in [20], among others, and in the Appendix A. These matrices will contain the filter parameters and the grid frequency \(\omega_{g}\).

2.2 On series compensator

The series compensator is also shown in Fig. 1 and it is, mainly, responsible for voltage unbalance, harmonics and voltage sag/swell compensation so that the load voltage is clean of disturbances. However, it could also compensate for reactive power, if required, although the compensation using the shunt converter is more obvious and natural. The series power converter is connected to the secondary of the series transformer through an LC filter. Table 2 summarizes the value of the parameters used for the series compensator in Fig. 1 where the leakage inductance of the transformer has been neglected, as in the rest of this paper.

Table 2 Series compensator output filter
Full size table

The shunt compensator will inject a controlled current in parallel with the load current. Therefore, the shunt compensator can be considered as a current disturbance in the series compensator model. Accordingly, the state-space model of the series compensator after Park’s Transformation is of the standard form:

$$\frac{{{\text{d}}\varvec{x}_{s} }}{{{\text{d}}t}} = \varvec{A}_{s} \varvec{x}_{s} + \varvec{B}_{s1} \varvec{u}_{s1} - \varvec{B}_{s2} \varvec{u}_{s2}$$
(3)
$$\varvec{y}_{s} = \varvec{C}_{s} \varvec{x}_{s} + \varvec{D}_{s1} \varvec{u}_{s1} + \varvec{D}_{s2} \varvec{u}_{s2}$$
(4)

where \(\varvec{x}_{s} = [i_{Lfd}\) \(i_{Lfq}\) \(v_{Cfd}\) \(v_{Cfq} ]^{t}\) is the vector of state variables; \(\varvec{u}_{s1} = [v_{id} ,v_{iq} ]^{t}\) is the input vector; \(\varvec{u}_{s2} = [i_{ld} - i_{lf2d} ,i_{lq} - i_{lf2q} ]^{t}\) is the disturbance vector; \(\varvec{y}_{s} = \left[ {v_{Cfd}\,\,v_{Cfq} } \right]\) is the output vector (to be controlled). As in (1) and (2) the model matrices contain the filter parameters and \(\omega_{g}\). They can be found in the literature (e.g. [19]) and are included in the Appendix A.

3 UPQC controller structure and design

According to (1)-(4), MIMO systems are produced by Park’s Transformation, including cross-coupling terms between variables of the \(d\) and \(q\) axes in both models. Besides, it is well known that there is a resonance in both models due to the second and third-order output filters. For example, with the parameters in Tables 1 and 2, the resonance frequencies are at 1.3 kHz and 923 Hz for the shunt compensator and for the series compensator, respectively. The main controller in both converters will have to look after the d-q axis decoupling and the output-filter resonance.

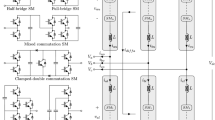
The proposed control structure in this paper is depicted in Fig. 2 where the main controller, the harmonic controller and the set-point calculation are clearly differentiated. The set-point vector for the series converter (\(\varvec{r}_{dq}^{se}\)) consists of the d-q components of the voltage to be injected by this converter, whereas the set-point vector for the shunt converter (\(\varvec{r}_{dq}\)) consists of the d-q components of the current to be injected by this converter. For analysis and design purposes, the plant model has been discretised using Backward-Euler rule and normalised in p.u. using the nominal voltage \(V_{N}\) and power \(S_{N}\) in Table 1, as base magnitudes.

Fig. 2
figure 2

Proposed control structure for a three-phase UPQC

Full size image

3.1 Design of main controllers

An LQR has been used as the main controller in Fig. 2 to eliminate the resonance and to minimise the coupling effect between \(d\) and \(q\) components. Since the fundamental-frequency components of all variables are DC after Park’s Transformation, an integral state has been added in each axis to ensure zero-error tracking of constant set points. In addition, two delays have been included to model the calculation delay and the measurement dynamics (anti-aliasing filters will be used in the prototype), resulting in two additional states in each axis. Figure 3 shows the discrete-time implementation of the LQR. The LQR seeks the optimal control of the form:

Fig. 3
figure 3

Discrete-time implementation of LQR (main controller)

Full size image
$$u_{dq} \left[ k \right] = - k_{opt} x\left[ k \right] = - \left[ {k_{a} , k_{int} , k_{ret} } \right]x\left[ k \right]$$
(5)

where \(k_{a}\) is the gain vector for the plant states; \(k_{int}\) is the gain vector for the integral states; \(k_{ret}\) is the gain vector of the delayed states. The gain vector \(k_{opt}\) minimizes the quadratic cost function:

$$J = \sum\limits_{i = 1}^{\infty } {x_{i}^{\text{T}} \varvec{Qx}_{i} } + \varvec{u}_{i}^{\text{T}} \varvec{Ru}_{i}^{\text{T}}$$
(6)

where the matrices \(\varvec{Q}\) and \(\varvec{R}\) have been chosen as diagonal matrices:

$$\left\{\begin{aligned}& \varvec{Q} = diag\left( {w_{1} , w_{2} , \ldots , w_{n} } \right) \hfill \\ &\varvec{R} = diag\left( {r_{11} ,r_{22} } \right) \hfill \\ \end{aligned}\right.$$
(7)

The elements of the diagonal of \(\varvec{Q}\) and \(\varvec{R}\) are set to 1 as the model is in p.u. with the only exception of the weights related to integral states which are all given the same value (\(w_{i}\)). This being the only design parameter of the LQR algorithm.

For example, Fig. 4 shows the simulated transient response of the \(d\)-axis output current (left) and the \(q\)-axis output current (right) in the shunt converter (\(i_{Lf2d}\) and \(i_{Lf2q}\), respectively) when there is a step input in the set-point signal of the \(d\) axis. The transients have been recorded for different values of \(w_{i}\) to show how the design parameter affects the closed-loop system speed. Clearly, the current \(i_{Lf2}\) responds as a well-damped first-order system, showing no resonance although there is a small cross-coupling effect between \(d\) and \(q\) axes.

Fig. 4
figure 4

Simulated transient response of \(i_{Lf2}\) using diferent values of \(w_{i}\)

Full size image

As the shunt compensator must ensure a constant DC-link voltage, the bandwidth of the shunt compensator main controller should be slightly higher than the bandwidth of the series compensator main controller. Therefore, \(w_{i}\) has been selected larger in the shunt compensator than in the series compensator. Coordination between series and shunt compensators was not addressed in the partial problems discussed in [19] and [20].

The open-loop and closed-loop frequency responses of the shunt compensator are shown in Fig. 5: ① the “Plant (\(d\) axis)” frequency response corresponds to the transfer function from the d-axis converter output voltage (\(v_{i}\)) to the d-axis variable to be controlled (\(i_{lf2}\)); ② the “Plant+LQR (\(d\) axis)” corresponds to the transfer function from the \(d\)-axis set point to the \(d\)-axis variable to be controlled; ③ the “Plant (cross-coupling)” frequency response corresponds to the transfer function from the \(d\)-axis converter input voltage to the \(q\)-axis variable to be controlled; ④ the “Plant+LQR (cross-coupling)” corresponds to the transfer function from the \(d\)-axis set point to the \(q\)-axis variable to be controlled. Figure 5 clearly shows that the resonance has been eliminated and the d-q axis cross-coupling has been greatly attenuated. Therefore, this cross-coupling will be neglected in the rest of the paper and the stability analysis for the harmonic controller is going to be done using the frequency response of the \(d\) axis with the LQR in place, only. Similar conclusions can be reached if the series compensator is investigated.

Fig. 5
figure 5

Open-loop and closed-loop frequency response of the shunt converter (d axis) and cross-coupling d to q axes

Full size image

In order to reduce the number of sensors required to control the UPQC, a linear quadratic estimator (LQE), commonly known as KF, has been used to estimate all but the output variables of the LC and LCL filters in Fig. 1. Since the KF is a linear filter in this case, it should not pose a heavy calculation burden. However, an industrial implementation should weigh the reliability improvement and the cost reduction given by the reduction of the number of sensors and the cost increment due to the choice of a microprocessor capable of handling the algorithm. Measurements have been used for only four variables, namelly: the PCC voltage \(v_{pcc}\), the shunt compensator output current \(i_{Lf2}\), the load voltage \(v_{l}\) and the load current \(i_{l}\). Meanwhile, the output voltage of the series compensator is calculated as \(v_{Cf} = v_{l} - v_{pcc}\). The KF used for the shunt compensator estimates \(i_{Lf1}\) and \(v_{Cf}\) and, similarly, the KF used for the series compensator estimates \(i_{Lf}\).

The KFs are based on stochastic versions of the plant models which include the process noise \(w\left[ k \right]\) to characterize the uncertainty in the model and the measurement noise \(v\left[ k \right]\), resulting a state-space model of the form:

$$x\left[ {k + 1} \right] = \varvec{A}_{d} x\left[ k \right] + \varvec{B}_{d} u\left[ k \right] + w\left[ k \right]$$
(8)
$$y\left[ k \right] = \varvec{C}_{d} x\left[ k \right] + \varvec{D}_{d} u\left[ k \right] + v\left[ k \right]$$
(9)

where \(\varvec{A}_{d}\), \(\varvec{B}_{d}\), \(\varvec{C}_{d}\), \(\varvec{D}_{d}\) are the discrete-time state-space matrices of the state-space matrices in (1)-(4). There will be a set of matrices for the shunt compensator and another one for the series compensator.

The updated KF estimates the state variables \(x\left[ k \right]\) using the available information of the measurements at sample \(k\) (usually called \(\hat{x}\left[ {k/k} \right]\)). The estimation of \(\hat{x}\left[ {k/k} \right]\) can be written in state-space form as:

$$\hat{x}\left[ {k + 1/k} \right] = \varvec{A}_{est} \hat{x}\left[ {k/k - 1} \right] + \varvec{B}_{est} \left[ {\begin{array}{*{20}c} {u\left[ k \right]} \\ {y\left[ k \right]} \\ \end{array} } \right]$$
(10)
$$\hat{x}\left[ {k/k} \right] = \varvec{C}_{est} \hat{x}\left[ {k/k - 1} \right] + \varvec{D}_{est} \left[ {\begin{array}{*{20}c} {u\left[ k \right]} \\ {y\left[ k \right]} \\ \end{array} } \right]$$
(11)

where

$$\left\{ {\begin{array}{ll} {\user2{A}_{{est}} = \user2{A}_{d} [\user2{I} - \user2{M}_{d} \user2{C}_{d} ]} \\ {\user2{B}_{{est}} = [\user2{B}_{d} \quad \user2{A}_{d} \user2{M}_{d} ]} \\ {\user2{C}_{{est}} = [\user2{I} - \user2{M}_{d} \user2{C}_{d} ]} \\ {\user2{D}_{{est}} = [{\mathbf{0}}\quad \user2{M}_{d} ]} \\ \end{array} } \right.$$
(12)

The gain vector \(\varvec{M}_{d}\) is calculated by minimizing the cost function:

$$J = \sum\limits_{i = 1}^{\infty } {[(x[k]_{i} - \hat{x}[k/k]_{i} )^{\text{T}} (x[k]_{i} - \hat{x}[k/k]_{i} )]}$$
(13)

In order to use a KF, one has to declare the variance of the process noise \(w\left[ k \right]\) and the variance of the measurement noise \(v\left[ k \right]\). The latter can be estimated looking available measurements. The former can be used as a design parameter. The name \(w_{kal}\) will be used for the variance of the process noise chosen. This parameter will be set to a number between 0 and 1 as a percentage of the confidence in the plant model and it is related to the speed of convergence of the state-variable estimation. Note that the KF is optional if the full state vector is measured.

Figure 6 shows the discrete-time implementation of the LQG.

Fig. 6
figure 6

LQG discrete-time implementation (main controller)

Full size image

3.2 Design of the harmonic controller

The harmonic controller used is depicted in Fig. 7. An efficient multiple synchronous reference frame (EMRF) controller as the one proposed in [19] is used in this paper due to its simplicity, low computational effort and frequency-adaptation capability.

Fig. 7
figure 7

EMRF harmonic controller

Full size image

In this case, the EMRF controller has been set to track harmonics at \(m = 6k \pm 1\) with \(k = 1,2, \ldots ,5\) on the three-phase electrical variables (voltages and currents). These are the typical harmonics present in power systems. After referring variables to the main SRF with Park’s Transformation using the position of the space vector of the PCC voltage, each of those harmonics is seen as a space vector rotating with an angular speed:

$$\omega_{n} = \overbrace {{\left( {i\cdot m - 1} \right)}}^{n}\omega_{g}$$
(14)

where \(m\) is the harmonic order; \(\omega_{g}\) is the grid frequency; \(i = 1\) for positive-sequence harmonics and \(i = - 1\) for negative-sequence harmonics. In addition, a special harmonic controller has been used for \(m = 1\) and \(i = - 1\) which corresponds to the negative-sequence components of the fundamental frequency.

In the EMRF approach, the error signal is calculated in the main SRF and rotated several times to refer it to the harmonic-synchronous reference frames (HSRF) which rotate with the angular speeds calculated in (14). The error for each harmonic \(n\) will show as a pair of DC values on the HSRF with angular speed \(\omega_{n}\) (\(dq,n\) reference frame) and can be easily treated there with an integrator (one for the \(d,n\) axis and another one for the \(q,n\) axis). The command signals calculated in each HSRF have to be rotated back to the main SRF to be added together. As shown in [19], the contribution of all integral controllers placed on the various HSRFs can be calculated in the main SRF using:

$$C_{dq} (s) = \sum\limits_{\forall n} {C_{dq,n} (s) = 2\sum\limits_{\forall n} {\left[ {k_{i} \frac{{a_{n} s - n\omega_{g} b_{n} }}{{s^{2} + (n\omega_{g} )^{2} }}} \right]} }$$
(15)

which has been discretised for analysis purposes using Tustin method with pre-warping giving:

$$C_{dq} (z) = \sum\limits_{\forall n} {\frac{{k_{i} }}{{n\omega_{g} }} \cdot \frac{{(c_{1} - c_{2} )z^{2} - 2c_{2} z - (c_{1} + c_{2} )}}{{z^{2} - 2z\cos (n\omega_{g} t_{s} ) + 1}}}$$
(16)

with \(c_{1}\) and \(c_{2}\) defined as:

$$\left\{ \begin{aligned} &c_{1} = a_{n} \sin \left( {n\omega_{g} t_{s} } \right) \hfill \\ &c_{2} = b_{n} \left( {1 - { \cos }\left( {n\omega_{g} t_{s} } \right)} \right) \end{aligned} \right.$$
(17)

where \(a_{n}\) and \(b_{n}\) are calculated with the frequency response of \(G_{dq}^{{\prime }} (z)\) in Fig. 8 and implemented in the matrix \(\varvec{\varUpsilon}_{n}^{ - 1}\) in Fig. 7 [19]. The use of \(\varvec{\varUpsilon}_{n}^{ - 1}\) ensures a phase margin of \(90^{\text{o}}\) at each harmonic frequency. Figure 9 shows the frequency response of the open-loop transfer funtion \(G_{dq} \left( z \right) = M_{dq}^{{\prime }} \left( z \right)/M_{dq} \left( z \right)\) in Fig. 8 for the shunt compensator and two different values of \(k_{i}\). The controller form in (15) is the sum of resonant controllers like those in [14] but the implementation using HSRFs makes the frequency adaptation straightforward by using the value of \(\omega_{g}\) estimated by the system PLL to carry out the frame rotation.

Fig. 8
figure 8

Open-loop block diagram for harmonic controller design

Full size image

The use of the same value of \(k_{i}\) for all harmonics is a reasonable strategy to ensure closed-loop stability: with the same value of \(k_{i}\) the gain margin is naturally increased as the frequency increases and only one value of \(k_{i}\) has to be designed, which is related to the speed of the transient response. Two different values of \(k_{i}\) have been used in Fig. 9 to illustrate the effect of \(k_{i}\) in the stability margins. The different phase margins are always close to 90° regardless the value of \(k_{i}\) and the minimum gain margin required is used to design \(k_{i}\). The same procedure has been carried out to design the harmonic controller for the series compensator. Gain margins of 10 dB have been chosen for the tests at the end of the paper.

Fig. 9
figure 9

Open-loop frequency response of \(G_{dq} \left( z \right)\) for the shunt converter (K i1 = 1 and K i2 = 7.9)

Full size image

Therefore, three parameters that have to be designed for each converter: \(w_{i}\) for the main controller, \(w_{kal}\) for the KF and \(k_{i}\) for the harmonic controller.

3.3 Set-point calculation

The set-point calculation block in Fig. 2 is used to handle the control objectives of the UPQC.

First of all, the shunt compensator has to compensate for the reactive power consumed by the load. Due to Park’s Transformation and the PLL synchronisation, the reactive power is directly related to the DC component of the \(q\) axis in all currents. Accordingly, the DC component of the set point \(i_{Lf2,q}^{ref}\) has to be set equal to the DC component of the load current \(i_{l,q}\), if the reactive power of the load has to be fully compensated for. Partial load reactive power compensation or over compensation are also possible using different set-point values of \(Q_{ref}\) and their corresponding values of \(i_{Lf2,q}^{ref}\).

Secondly, to ensure a constant DC voltage, a closed-loop control of the DC-voltage is mandatory in the shunt compensator. Similarly to the reactive power, the active power is directly related to the DC component of the \(d\) axis of the grid, load and filter currents. A PI controller can be designed as in [21], to calculate the required instantaneous active power to be injected. Then, the DC component of the set point \(i_{Lf2,d}^{ref}\) can be obtained as in Fig. 10a, where the output of the PI is divided by the voltage at the PCC to calculate the \(i_{Lf2,d}^{ref}\).

Fig. 10
figure 10

Set-point calculation

Full size image

Finally, the shunt compensator has to tackle the harmonic currents consumed by the load to reduce the harmonic contents of the grid currents. The DC components of the load currents in the main SRF are subtracted from the original currents and used as the harmonic components of the set point \(i_{Lf2,dq}^{ref}\) as shown in Fig. 10a.

The series compensator has two main objectives. First of all, it has to compensate for voltage sags and voltage swells. The in-phase compensation method has been implemented in this paper by using [1 0] (ideal voltage) minus the actual PCC voltage as the set point for the capacitor voltage \(v_{Cf,dq}\) in Fig. 10b. Nevertheless, other compensation methods can be easily included in the set-point calculation block. The harmonic controller of the series compensator will look after the harmonic distortion of the load voltage since [1 0] is used as the ideal voltage to be imposed on the load.

4 Experimental results

A three-phase UPQC prototype like in Fig. 1 has been built to illustrate the performance of the proposed control strategy. The full control algorithm was implemented in Matlab/Simulink and, then, it was downloaded into a dSpace 1103 platform. Two 15 kVA Semikron SKS 22F B6U two-level, three-leg Voltage Source Converters were used in the prototype. All electrical variables were measured by a Yokogawa DL850 oscilloscope and they were also stored in the dSpace platform for further analysis. The electrical grid was emulated using a controlled 12 kVA three-phase amplifier Pacific Power Source 3120 AMX.

First of all, the steady-state performance of the UPQC was challenged when, both, the grid voltage and the load current had harmonics. In the experiment recorded the grid voltage had 5th and 7th harmonics and the load consisted of a three-phase rectifier with an inductive filter in the DC side. Figure 11 shows the steady-state response when the UPQC is cleaning both voltage and current harmonics.

Fig. 11
figure 11

Steady-state response during voltage and current harmonic compensation

Full size image

Voltage flicker is considered as one of the most severe power quality problems (especially in loads like electrical arc furnaces). The UPQC can easily compensate for voltage flicker using only the main controller in Section 3. Figure 12 shows the steady-state response measured with the osciloscope when the UPQC is compensating for voltage flicker.

Fig. 12
figure 12

Steady-state response during voltage flicker compensation

Full size image

The UPQC can also tackle sags or swells in the grid voltage using only the main controller described in Section 3. The adjustment of the control system bandwidth will determine the transient response of the device. For example, Fig. 13 shows the UPQC performance when a voltage sag takes place at t = 1.61 s. The series compensator restores the load voltage in less than 10 ms. In the voltage sag/swell compensation experiments, a three-phase rectifier with a large L DC filter was the sensitive load to be protected. The grid current is sinusoidal because the shunt converter is filtering out the load current harmonics. Since the shunt converter is close to the disturbing load, the current harmonics do not affect the series transformer, either.

Fig. 13
figure 13

Transient response during a voltage sag

Full size image

If the grid voltage is unbalanced, a 100 Hz harmonic will appear after Park’s Transformation into the main SRF (\(dq\)). Therefore, the series compensator must be prepared to eliminate the 2nd harmonic from the load voltage. Figure 14 shows the steady-state response when the grid voltage is unbalanced. Clearly, the load voltage and grid currents are balanced.

Fig. 14
figure 14

Steady-state response when grid voltage is unbalanced

Full size image

Finally, an experiment has been carried out with varying grid frequency. Figure 15 shows the transient response when the grid frequency changes from 50 to 51 Hz. In spite of this change, the harmonic contents in the load voltage and grid currents is almost zero during the transient and at the new steady state.

Fig. 15
figure 15

Transient response during a grid frequency change from 50 to 51 Hz

Full size image

Data in Figs. 13 and 14 have been recorded from the prototype with the dSpace platform and plotted with Matlab.

5 Conclusion

This paper has presented experimental results of a UPQC using a simplified control structure, in which only three parameters have to be designed. The main conclusions can be summarised as follows:

  1. 1)

    The hiralchical control structrue for a UPQC has been presented showing how series and shunt compensators have to be coordinated.

  2. 2)

    The two electronic converter have been controlled with a relatively low constant switching frequency and the number of sensors have been reduced using a KF.

  3. 3)

    An LQR is used as the main controller to deal with power flow issues. It reduces the cross-coupling between \(d\) and \(q\) axes and suppresses the resonance of the filters.

  4. 4)

    A multiple SRF-based controller is used as the harmonic controller to compensate for both voltage and current harmonics. Unbalance in the grid voltage and load currents can be easily treated within the harmonic framework. It has been shown that the harmonic controller (in the series and in the shunt compensators) works properly even under grid-frequency variations due to the frequency-adaptation capability of the ESRF-based controller. This feature was never demostrated in a UPQC before.

  5. 5)

    A laboratory prototype of a three-phase UPQC has been built to test all the studied functionalities. The experimental results show a very good performance when compensating for power-quality issues.