1 Introduction

1.1 Motivation

The emergence and significant penetration of distributed generators (DGs) are transforming conventional passive distribution networks (PDNs) into active distribution networks (ADNs). Lots of new problems (e.g., overvoltage, reversed flows and overflows), however, have been brought into the distribution networks. These new challenges and the tendency moving towards smart distribution systems both require more comprehensive and accurate knowledge of the system states to implement real-time monitoring and active control for ADNs.

State estimation (SE) [1, 2] provides a snapshot of network operating conditions from continuously updated measurements collected by supervisory control and data acquisition (SCADA) systems. SE has been a crucial tool for transmission system energy management systems (EMSs), where a variety of advanced applications for the economic, secure and reliable operation of power systems depend on the real-time states calculated by SEs. Analogously, for smart distribution systems, the quick and sharp fluctuations of DG outputs [3] and the frequent change of the network topology urge the distribution system operators to assess the operating conditions in an accurate and fast manner. Consequently, there is an increasing need for SEs that can enable enhanced grid situational awareness in the smart distribution system applications. To fulfill this target, three-phase SEs should be performed since distribution systems are inherently unbalanced with their unbalanced loads and network parameters [4].

1.2 Literature review

Previous works on conventional passive distribution network state estimation (PDNSE) can be summarized, roughly speaking, as three aspects: ① The choice of state variables [5–7]. Apart from choosing voltage as state variables, branch-current based SEs were implemented to improve the computational efficiency and reduce the sensitivity to network parameters [5–7]; ② The choice of state estimator [8–10]. In [8, 9], robust estimators were investigated to eliminate bad data out of redundant measurements. Gol and Abur [8] proposed a least absolute value (LAV) estimator for a three-phase SE. In [9], a new equivalent weight function was developed. Singh et al. [10] investigated the choice of state estimators for distribution systems, and concluded that weighted least squares (WLS) based SE was the most appropriate method because of the low redundancy levels. ③ Measurement configuration and observability issues [11–13]. Since distribution networks are short of sufficient metering infrastructures, load estimation [9, 11] based on prior knowledge of load variation pattern was carried out to function as pseudo -measurements. Meanwhile, depending heavily on the low-performance pseudo-measurements, the SE’s quality is probably too low to ensure an effective network management and control. As regards this, considerable efforts have been devoted to determine the proper number and placement of measurement instruments to guarantee the network observability, minimum investments and required accuracy [12, 13].

In comparison with PDNSE, the major issue for active distribution network state estimation (ADNSE) lies in the modeling of DGs. A single-phase SE for distributed networks integrated with DGs was performed in [14]. In [15], the DG units were modeled as PQ bus injection, without any detailed models of DGs. In [16], sequence-based models for different types of DGs were proposed. Pseudo- measurements for the DG three-phase total outputs, obtained from historical database or weather forecast, were set for unmonitored DGs in [16, 17]. Moreover, the phase outputs of DGs were determined with phase-based averaging. However, this phase-based averaging approach degrades the SE accuracy because the phase outputs of DGs largely depend on the unbalanced operating conditions [18, 19]. It is often assumed that the three-phase output powers of DGs are balanced. However, that is not always the case in light of the unbalanced interfacing conditions. To conclude, the asymmetric characteristics of distribution networks or DG three-phase outputs have not been well considered.

Another intractable challenge for ADNSE is that, due to the typically large scale of distribution networks, the unbalanced three-phase network structure and the extensive integration of DGs, significant computational efforts can be required [20]. Furthermore, the high resistance/resactance (R/X) ratios of distribution network branches could lead to worrying numerical stability issues for ADNSE. The SE numerical stability issue was well addressed by convex semidefinite programming proposed in [21], but with a considerable computation burden. Compared with integrated state estimation (ISE), multi-area distributed state estimation (DSE), in which the large-scale network is divided into several subareas and the SE in each area is performed in parallel, shows a higher computational efficiency and a better numerical stability. Numerous studies have provided elegant foundations for DSE at the transmission level [22–27]. Interested readers can refer to [22] for state of the art of DSE methods in multi-area transmission systems. But the works dealing with distribution network DSE are somewhat limited [28–30]. In [28], a new two-step DSE procedure was performed in distribution networks with additional measurement devices to be shared among neighboring areas. Agent-based DSE methods were discussed in [29] and [30].

1.3 Contribution and paper organization

Based on the above discussion, this work proposes an innovative distributed three-phase state estimation method for unbalanced ADNs. First, detailed three-phase steady-state models of DGs have been presented with consideration towards the asymmetric characteristics of DG three-phase outputs. Next, a feasible strategy to set pseudo-measurements for unmonitored DGs was employed. After that, we developed a multi-area DSE scheme based on the concept of extended sub-areas and the augmented Lagrangian relaxation method. Meanwhile, the information exchanged between adjacent areas has been interpreted as equivalent pseudo-measurements for extended boundary buses. The primary contributions of this paper can be summarized as:

  1. 1)

    By taking into account of unbalanced DG phase outputs, the accuracy of SE for ADNs integrated with multi-type DGs is ensured.

  2. 2)

    A fully distributed state estimator is proposed, in which only a very limited data is exchanged between neighboring areas and no central processor is needed.

  3. 3)

    Even though the states of DGs and extended boundary buses were added into state variables, the observability for DSE still holds on.

  4. 4)

    The DSE framework developed in this research can simulate large-scale unbalanced networks and produce a fast, accurate and reliable solution.

For the remainder of this paper, the WLS-based SE for PDNs model is introduced in Section 2. In Section 3, SE for unbalanced ADNs integrated with different types of DGs is presented. Section 4 describes the DSE formulations. After that, Section 5 presents test results and their interpretations. Finally, Section 6 draws the conclusions.

2 WLS-based SE for PDNs

WLS provides the maximum likelihood estimation by solving the following optimization problem:

$$\mathop {\hbox{min} }\limits_{{\mathbf{x}}} \;J(\varvec{x}) = ({{\varvec{z}}} - h({\varvec{x}}))^{\text{T}} \varvec{R}^{ - 1} ({\varvec{z}} - h({\varvec{x}}))$$
(1)

where \(\varvec{z} \in \Re^{m}\) is the measurement vector (m denotes the number of measurements); \({\user2{ x}} \in \Re^{n}\) denotes the state variable vector (n represents the number of buses); \(R = {\text{diag}}\{ \sigma_{1}^{2} \,,\,\sigma_{2}^{2} \,,\, \cdots ,\,\sigma_{m}^{2} \,\}\); \(\sigma\)is the standard deviation; \(\varvec{R}^{ - 1}\) is the weighted matrix; \(h( \cdot )\) is a nonlinear function relating x and z; \(m \ge n\) is a necessary condition for an observable system in which the state variables x can be uniquely obtained from the measurements z.

In this work, three-phase complex voltages have been selected as state variables (the root node is taken as the slack node, and its voltage is constant):

$$\varvec{x} = [\varvec{U}^{\text{abc}} \,\,\varvec{\delta}^{\text{abc}} ]^{\text{T}}$$
(2)

where \(\varvec{U}^{\text{abc}}\) and \(\varvec{\delta}^{\text{abc}}\) are the three-phase voltage magnitude and angle, respectively.

As for the measurements in distribution networks, virtual measurements at the tied nodes (zero injected power) and pseudo-measurements should be exclusively included considering the poor number of real-time measurements. Fortunately, promising developments in phasor measurement units (PMUs) [8] and smart meters [31] are expected to facilitate the SE at the distribution levels.

It is known that the WLS-based SE problem (1) is inherently a nonlinear optimization problem, to solve it the first-order optimality conditions should be satisfied at the beginning. Then, the Gauss–Newton method is used to linearize the first order optimality conditions. Finally, the iterative formulation of (1) can be expressed as:

$$\left\{\begin{aligned}&{\Delta \varvec{x}^{(k)} = \left[ {\varvec{H}^{\text{T}} (\varvec{x}^{(k)} )\varvec{R}^{{{ - }1}} \varvec{H}(\varvec{x}^{(k)} )} \right]^{ - 1} \varvec{H}^{\text{T}} (\varvec{x}^{(k)} )\varvec{R}^{{{ - }1}} \left( {\varvec{z} - h\left( {\varvec{x}^{(k)} } \right)} \right)}\\&{\varvec{x}^{(k + 1)} = \varvec{x}^{(k)} + \Delta \varvec{x}^{(k)} }\end{aligned} \right.$$
(3)

where k denotes the iteration index and H is the measurement Jacobian maxtrix.

3 Three-phase SE for unbalanced ADNs

A model considering the asymmetric characteristics of DG three-phase outputs is proposed to perform three-phase SE for unbalanced ADNs. Additionally, the operating states of DGs have been added into the state variables. Furthermore, a feasible strategy setting pseudo-measurements for unmonitored DGs is presented to guarantee the observability of ADNs.

3.1 Modeling of DGs

Motivations to present a detailed three-phase DG model include:

  1. 1)

    In engineering practice, the total three-phase power outputs are specified for each DG, but cannot be directly treated as SE measurements.

  2. 2)

    A situation, where the total three-phase power outputs of DGs are within their permissive limits but individual phase outputs are overloaded, could happen under unbalance operating conditions. As such, individual phase outputs of DGs should be accurately estimated when the total three-phase outputs are specified.

Generally, there are two ways for DGs connecting to ADNs (note that single-phase and two-phase DGs are not considered in this article):

  1. 1)

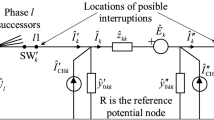
    DGs (e.g. the wind power and hydropower) are directly connected to ADNs through a synchronous or induction generator. The model of DGs directly connecting to ADNs is shown in Fig. 1.

    Fig. 1
    figure 1

    Model of DGs connected to the grid directly

    Full size image
  2. 2)

    DGs (e.g. solar PVs, fuel cells, doubly-fed induction generators (DFIGs), and storages) are integrated into ADNs through the pulse width modulation (PWM) voltage source converter (VSC) [32]. The model of DGs connecting to ADNs through PWM converters is shown in Fig. 2. The primary DG sources are not directly included in the model since it is assumed that DG outputs are perfectly controlled by PWM converters.

    Fig. 2
    figure 2

    Model of DGs connected to the grid through PWM

    Full size image

In Figs. 1 and 2, \({E}_{0}\) and \({\delta}_{0}\) are the voltage magnitude and angle of DGs (in Fig. 1) or PWM converters on the AC side (in Fig. 2); \({P}_{\text{in}}\) and \({Q}_{\text{in}}\) are the three-phase total active and reactive powers injected into the AC network; \({P}_{0}\) and \({Q}_{0}\) are the three-phase total active and reactive outputs of DGs (in Fig. 1) or PWM converters on the AC side (in Fig. 2); \({P}_{\text{DC}}\) and \({U}_{\text{DC}}\) are the power and voltage of PWM converters on the direct current (DC) side; \({M}_{0}\) is the modulation coefficient of PWM converters; \(\varvec{P}_{\text{L}}^{\text{abc}}\) and \(\varvec{Q}_{\text{L}}^{\text{abc}}\) are the complex loads connected to the AC network; \(\varvec{U}_{\text{AC}}^{\text{abc}} \,\angle\,\varvec{\delta}_{\text{AC}}^{\text{abc}}\) is the complex voltage of the AC bus to which the DG is connected; \(r_{\varphi }\) (\(\varphi \in \{ {\text{a}},{\text{b}},{\text{c}}\}\)) is the equivalent resistance for power loss; \(\varvec{x}_{\varphi }\) (\(\varphi \in \{ {\text{a}},{\text{b}},{\text{c}}\}\)) is the equivalent reactance for the transformer and VSC filter.

It should be noted that nodal voltages of both directly connected DGs as presented in Fig. 1 (with balanced designs) and PWM converters as presented in Fig. 2 (with symmetric switching) are symmetric. As such, \({E}_{0}\) and \({\delta}_{0}\) are single-phase state variables. However, due to the unbalanced network parameters and loads, the states for the AC buses need to be represented by the three-phase state variables \(\varvec{U}^{\text{abc}}\) and \(\varvec{\delta}^{\text{abc}}\).

In accordance with the detailed DG models proposed here, the operating states of DGs are included in state variables as:

$$\varvec{x}_{\text{AC}} = [{\varvec{x}}\,\,{E}_{0} \,\,{\delta}_{0} ]^{\text{T}}$$
(4)

where \(\varvec{x}_{\text{AC}}\) is the augmented state variable vector on the AC side.

With new state variables of DGs introduced, conventional measurements cannot guarantee the observability of ADNs because it is not realistic to equip all DGs with real-time metering devices. As a result, the system operators might lose the ability to be thoroughly aware of ADN operating conditions. Given this, it is of significant importance to effectively observe unmonitored DGs; this will be analyzed in the next subsection.

3.2 Set pseudo-measurements for unmonitored DGs

Let \({\varvec{z}}_{\text{DG}}\) denote the pseudo-measurements setting for unmonitored DGs. Then, the augmented measurements on the AC side become:

$${\varvec{z}}_{\text{AC}} = [{\varvec{z}}\,\,{\varvec{z}}_{\text{DG}} ]^{\text{T}}$$
(5)

where \(\varvec{z}_{\text{AC}}\) is the augmented measurement vector.

Since the augmented state variables \(\varvec{x}_{\text{AC}}\) contain additional state variables \({E}_{0}\) and \({\delta}_{0}\), the dimension of the newly introduced measurements \({\varvec{z}}_{\text{DG}}\) needs to satisfy:

$$\dim (\varvec{z}_{\text{DG}} ) \ge \dim ([{E}_{0} \,\,{\delta}_{0} ])$$
(6)

In order to satisfy (6), one feasible and realistic strategy to set pseudo-measurements for the unmonitored DGs connecting to ADNs either directly or through PWM converters is illustrated as follows.

3.2.1 DGs connected to ADNs directly

The three-phase total active outputs \({P}_{0}\) of DGs can be estimated from historical database or forecasted weather data [16, 17]. After that, according to \({P}_{0}\), the three-phase total reactive outputs \({Q}_{0}\) of DGs can be calculated from the P–Q diagram or the power factor of DGs. Therefore, \({P}_{0}\) and \({Q}_{0}\) can be included in the pseudo-measurements \(\varvec{z}_{\text{DG}}\) as:

$$\varvec{z}_{\text{DG}} = [{P}_{0} \,\,{Q}_{0} ]$$
(7)

The pseudo-measurements \(\varvec{z}_{\text{DG}}\) in (7) can be explicitly related to the augmented state variables \(\varvec{x}_{\text{AC}}\) as follows:

$$\begin{aligned} P_{0} &= \sum\limits_{{\varphi \in \{\text{ a,\,b,\,c\}} }} {E_{0}^{2} g^{\varphi } - E_{0} U_{\text{AC}}^{\varphi } g^{\varphi } \cos \left( {\delta_{0}^{\varphi } - \delta_{\text{AC}}^{\varphi } } \right)} \hfill \\ &\quad- \sum\limits_{{\varphi \in \{ \text{a,\,b,\,c\}} }} {E_{0} U_{\text{AC}}^{\varphi } b^{\varphi } \sin \left( {\delta_{0}^{\varphi } - \delta_{\text{AC}}^{\varphi } } \right)} \hfill \\ \end{aligned}$$
(8)
$$\begin{aligned} Q_{0} &= \sum\limits_{{\varphi \in \{\text{ a,\,b,\,c\}} }} -\,{E_{0}^{2} b^{\varphi } + E_{0} U_{\text{AC}}^{\varphi } b^{\varphi } \cos (\delta_{0}^{\varphi } - \delta_{\text{AC}}^{\varphi } )} \hfill \\ &\quad- \sum\limits_{{\varphi \in \{ \text{a,\,b,\,c\}} }} {E_{0} U_{\text{AC}}^{\varphi } g^{\varphi } \sin (\delta_{0}^{\varphi } - \delta_{\text{AC}}^{\varphi } )} \hfill \\ \end{aligned}$$
(9)

where \(\delta_{0}^{a} = \delta_{0}\), \(\delta_{0}^{b} = \delta_{0} - 120^{ \circ }\), and \(\delta_{0}^{c} = \delta_{0} + 120^{ \circ }\). \(g = r/\left( {r^{2} + x^{2} } \right)\), and \(b = - x/\left( {r^{2} + x^{2} } \right)\).

Analogous to the pseudo-measurements for unmonitored loads, a relatively small SE weight should be set for the pseudo-measurements \(\varvec{z}_{\text{DG}}\) with a wide range of uncertainty.

3.2.2 DGs connected to ADNs through PWM

DGs, connecting to ADNs through PWM converters, operate in different modes depending on the control strategies of PWM converters. The PWM converters link the AC side with the DC side and can control the states of both the DC and AC side. It is worth mentioning that control of individual phase outputs is not possible. Instead, the total of three-phase outputs are much more easily controllable in practice [18, 19]. In this paper, the controlled states of DGs are set as pseudo-measurements, and two common control strategies are considered:

  1. 1)

    P–Q mode

When DGs (e.g. storages and fuel cells) operate under this mode, the three-phase total active and reactive power \({P}_{\text{in}}\), \({Q}_{\text{in}}\) injected into the AC network are specified. Accordingly, \(\varvec{z}_{\text{DG}}\) can be developed as:

$$\varvec{z}_{\text{DG}} = [{P}_{\text{in}} \,\,{Q}_{\text{in}} ]$$
(10)

As with (8) and (9), the following equations relating \(\varvec{z}_{\text{DG}}\) with \(\varvec{x}_{\text{AC}}\) can be obtained:

$$\begin{aligned} P_{\text{in}} &= \sum\limits_{{\varphi \in \{ {\text{a}},{\text{b}},{\text{c}}\} }} { -\, \left( {U_{\text{AC}}^{\varphi } } \right)^{2} g^{\varphi } + U_{\text{AC}}^{\varphi } E_{0} g^{\varphi } \cos \left( {\delta_{\text{AC}}^{\varphi } - \delta_{0}^{\varphi } } \right)} + \hfill \\ &\quad\sum\limits_{{\varphi \in \{ {\text{a}},{\text{b}},{\text{c}}\} }} {U_{\text{AC}}^{\varphi } E_{0} b^{\varphi } \sin \left( {\delta_{\text{AC}}^{\varphi } - \delta_{0}^{\varphi } } \right)} \hfill \\ \end{aligned}$$
(11)
$$\begin{aligned} Q_{\text{in}} &= \sum\limits_{{\varphi \in \{ {\text{a}},{\text{b}},{\text{c}}\} }} {\left( {U_{\text{AC}}^{\varphi } } \right)^{2} b^{\varphi } } - U_{\text{AC}}^{\varphi } E_{0} b^{\varphi } \cos \left( {\delta_{\text{AC}}^{\varphi } - \delta_{0}^{\varphi } } \right) + \hfill \\ &\quad \sum\limits_{{\varphi \in \{ {\text{a}},{\text{b}},{\text{c}}\} }} {U_{\text{AC}}^{\varphi } E_{0} g^{\varphi } \sin \left( {\delta_{\text{AC}}^{\varphi } - \delta_{0}^{\varphi } } \right)} \hfill \\ \end{aligned}$$
(12)
  1. 2)

    \(U_{\text{DC}} - Q\)mode

Under this control strategy, the voltage \({U}_{\text{DC}}\) of PWM converters on the DC side and the reactive power \({Q}_{\text{in}}\) injected into the AC network are set as given values. As \({{U}}_{\text{DC}}\) cannot be treated as measurements for AC networks straightforwardly, the equality constraints of the DC and AC side of PWM converters are given as:

$${P}_{0} = {P}_{\text{DC}} = f({U}_{\text{DC}} )$$
(13)
$${E}_{0} = k_{0} M_{0} {U}_{\text{DC}}$$
(14)

where\(k_{0} = \sqrt 3 /\left( {2\sqrt 2 } \right)\), and f represents the power-voltage nonlinear model on the DC side which can be understood as DC power flow (PF) equations.

In DC transmission networks, it needs an iterative solution of PF or SE as in AC networks. A DC network with DGs and PWM converters is relatively simple; the DC power \({P}_{\text{DC}}\) of the PWM converter on the DC side is independent of the states on the AC side and can be derived without any iterations. Thereby, one can get \({P}_{0}\) from \({U}_{\text{DC}}\) based on (13), and \(\varvec{z}_{\text{DG}}\) can be developed as:

$$\varvec{z}_{\text{DG}} = [{P}_{0} \,\,{Q}_{\text{in}} ]$$
(15)

In this case the mathematical formula between \(\varvec{z}_{\text{DG}}\) and \(\varvec{x}_{\text{AC}}\) can be referred to (8) and (12).

The actual states of the DGs controlled by PWM are very close to their given values. Given this, the accuracy of the pseudo-measurements \(\varvec{z}_{\text{DG}}\) obtained from (10) or (15) is high.

For each DG connecting to ADNs, a pair of new variables (\({E}_{0}\) and \({\delta}_{0}\)) is added into state variables. Correspondingly, based on (7), (10), or (15), two pseudo-measurements \(\varvec{z}_{\text{DG}}\), are introduced. Thereby, the following relationship between new variables and pseudo-measurements for DGs is given by:

$$\dim (\varvec{z}_{\text{DG}} ) = \dim ([{E}_{0} \,\,{\delta}_{0} ])$$
(16)

If there are additionally real-time measurements for DGs, it will produce a redundancy for DGs. Thus, by means of setting pseudo-measurements for DGs as illustrated above, the ADN integrated with DGs is observable.

In addition, for the DGs connected to ADNs through PWM converters, after the convergence of WLS-based ADNSE, the states of PWM converters (\({M}_{0}\)) and the states on the DC side (\({P}_{\text{DC}}\) and \({U}_{\text{DC}}\)) can be calculated from the known \({E}_{0}\) and \({P}_{0}\) based on (13)–(14).

4 Multi-area DSE for distribution networks

A fully distributed state estimator for multi-area distribution networks is described in this section. In a DSE scheme, each local subarea performs its own SE and communicates with neighboring areas for the exchange of border bus information. The proposed DSE method is on the premise of the following assumptions

  1. 1)

    The subarea division of the whole distribution networks is based on the geographical or topological criteria; each subarea can contain multiple DGs.

  2. 2)

    Neighboring areas share at least one bus and can exchange some amounts of border bus information.

  3. 3)

    Each subarea has an independent control center, e.g. distribution system operators or virtual power plants, to be responsible for carrying out SE and communicating with neighboring areas.

4.1 Extended areas of distribution networks

For simplicity, the decomposition of two adjacent areas K and L is illustrated as shown in Fig. 3. In Fig. 3, original areas K and L are two neighboring subareas; buses 1 and 2 are the boundary buses and belong to areas K and L, respectively. After decomposition, the original interconnected areas K and L are decomposed into extended areas K and L including all external boundary buses (bus 1 or bus 2). As established on the copies of boundary buses, this achieves area decoupling.

Fig. 3
figure 3

Concept of extended areas

Full size image

As the measurements in ADNs are rather limited, the designed DSE scheme should take full advantage of boundary bus and line measurements. Fortunately, it is easy to deal with the boundary measurements for the proposed network decomposition scheme for which all boundary buses are included in the extended areas. The conventional boundary measurement processing method [23] that the related boundary topology, network parameters and local SE results to the central coordinator can be initially avoided.

Let \(\varvec{x}_{K} [L]\) and \(\varvec{x}_{L} [K]\) be the boundary sub-variables of the extended areas K and L. For example, in Fig. 3, \(\varvec{x}_{K} [L]\) (or \(\varvec{x}_{L} [K]\)) consists of the three-phase bus voltages of {1, 2}. For a valid solution, neighboring areas must consent on the boundary sub-variables:

$$\varvec{x}_{K} [L] = \varvec{x}_{L} [K]$$
(17)

Next, the SE problem between neighboring subareas K and L is given as follows:

$$\mathop {\hbox{min} }\limits_{{({\mathbf{x}}_{K} ,\,\,{\mathbf{x}}_{L} )}} \;\{ J_{K} (\varvec{x}_{K} ) + J_{L} (\varvec{x}_{L} )|\varvec{x}_{K} [L] = \varvec{x}_{L} [K]\}$$
(18)

where \(\varvec{x}_{K}\) and \(\varvec{x}_{L}\) are the augmented state variables for the extended areas K and L, respectively.

4.2 Augmented Lagrangian relaxation

To solve the optimization problem (18), the equality constraint \(\varvec{x}_{K} [L] = \varvec{x}_{L} [K]\) needs to be dualized. Moreover, the augmented Lagrangian relaxation [26, 33] with a quadratic penalty term is introduced to improve the convergence property. As a result, the augmented Lagrangian function for (18) becomes

$$\mathop {\hbox{min} }\limits_{{(\varvec{x}_{K} ,\,\,\varvec{x}_{L} ,\,\,\varvec{\lambda},\;\alpha )}} \left\{ \begin{aligned} J_{K} (\varvec{x}_{K} ) + J_{L} (\varvec{x}_{L} ) +\varvec{\lambda}^{\text{T}} (\varvec{x}_{K} [L] - \varvec{x}_{L} [K]) \hfill \\ \;\quad \;\;\;\; + \,\alpha ||\varvec{x}_{K} [L] - \varvec{x}_{L} [K]||_{2}^{2} \hfill \\ \end{aligned} \right\}\;$$
(19)

where \(\varvec{\lambda}\) is the Lagrangian multiplier vector, and \(\alpha\) is a positive penalty factor.

The problem (19) cannot be decomposed directly because the same augmented Lagrangian function couples the SE tasks across areas K and L. To enable a fully distributed scheme, the block coordinate descent (BCD) method is adopted. This will yield two separate sub-problems (20)–(21) and a multiplier update (22) as:

$$\varvec{x}_{K}^{(t + 1)} = \arg \mathop {\hbox{min} }\limits_{{{\varvec{x}}_{K} }} \;\left\{ \begin{aligned} J_{K} (\varvec{x}_{K} ) + \left( {\varvec{\lambda}^{(t)} } \right)^{\text{T}} \left( {\varvec{x}_{K} [L] - \varvec{x}_{L} [K]^{(t)} } \right) \hfill \\ \;\quad \;\;\;\;\,\; + \;\frac{{\alpha^{(t)} }}{2}||\varvec{x}_{K} [L] - \varvec{x}_{L} [K]^{(t)} ||_{2}^{2} \hfill \\ \end{aligned} \right\}$$
(20)
$$\varvec{x}_{L}^{(t + 1)} = \arg \mathop {\hbox{min} }\limits_{{{\varvec{x}}_{L} }} \left\{ \begin{aligned} J_{L} (\varvec{x}_{L} ) + (\varvec{\lambda}^{(t)} )^{\text{T}} (\varvec{x}_{K} [L]^{(t + 1)} - \varvec{x}_{L} [K]) \hfill \\ \;\quad \;\;\;\;\,\; + \;\frac{{\alpha^{(t)} }}{2}||\varvec{x}_{K} [L]^{(t + 1)} - \varvec{x}_{L} [K]||_{2}^{2} \hfill \\ \end{aligned} \right\}\;$$
(21)
$$\varvec{\lambda}^{{(t{ + }1)}} { = }\,{\varvec{\lambda}}^{(t)} { + }\eta^{(t)} \left( {\varvec{x}_{K} [L]^{(t + 1)} - \varvec{x}_{L} [K]^{(t + 1)} } \right)$$
(22)

where t represents the iteration number; and \(\eta^{(t)}\) is a step size parameter.

Note that the augmented Lagrangian relaxation here severs as a local algorithm as \(J_{K} (\varvec{x}_{K} )\) and \(J_{L} (\varvec{x}_{L} )\) are nonconvex (nonlinear power flow equations). Based on the distributed procedure (20)–(22), neighboring subareas K and L solve (20) and (21) independently. Meanwhile, only a very limited boundary information (\(\varvec{x}_{K} [L]^{(t)}\) or \(\varvec{x}_{L} [K]^{(t)}\)) needs to be exchanged between subareas K and L at each successive iteration. The exchanges can be implemented in a fully distributed architecture.

4.3 Pseudo-measurements for extended boundary buses

To narrow the gap between the proposed DSE scheme (20) or (21) and the ISE scheme (1), the DSE problem (20) for subarea K can be rewritten as follows (the constant term is neglected)

$$\varvec{x}_{K}^{(t + 1)} = \arg \mathop {\hbox{min} }\limits_{{{\varvec{x}}_{K} }} \;\left\{ {J_{K} (\varvec{x}_{K} ) + \frac{{\alpha^{(t)} }}{2}||\varvec{z}_{K}^{\text{pse}} - \varvec{x}_{K} [L]||_{2}^{2} } \right\}$$
(23)
$${\varvec{z}}_{K}^{\text{pse}} = \varvec{x}_{L} [K]^{(t)} - \frac{1}{{\alpha^{(t)} }}\varvec{\lambda}^{(t)}$$
(24)

where \({\varvec{z}}_{K}^{\text{pse}}\) is the introduced measurement vector for extended area K.

Comparing the WLS formulation (1) with the second term of (23), it is noted that \(\varvec{z}_{K}^{\text{pse}}\) can be understood as the equivalent pseudo-measurements for extended subareas K. Here the pseudo-measurements \(\varvec{z}_{K}^{\text{pse}}\) whose SE weight is \(\alpha /2\) have a linear relationship with \(\varvec{x}_{K} [L]\).

Similarly, the pseudo-measurements \(\varvec{z}_{L}^{\text{pse}}\) for extended subareas K corresponding to (21) can be defined as

$$\varvec{z}_{L}^{\text{pse}} = \varvec{x}_{K} [L]^{(t + 1)} + \frac{1}{{\alpha^{(t)} }}\varvec{\lambda}^{(t)}$$
(25)

Under the DSE scheme illustrated above, the dimension of the pseudo-measurements and the boundary state variables for extended subareas is always equal

$$\dim (\varvec{z}_{K}^{\text{pse}} ) = \dim (\varvec{x}_{K} [L])\;{\rm or}\;\dim (\varvec{z}_{L}^{\text{pse}} ) = \dim (\varvec{x}_{L} [K])$$
(26)

Thus, for each pair of neighboring areas K and L, the proposed DSE scheme will keep the observability of the system. There is no further requirement for boundary measurement redundancy as long as local SEs or ISEs are observable. The proposed multi-area DSE procedure is detailed in Algorithm 1. Notice that the penalty factor \(\alpha\) is updated by \(\alpha^{(t)} = \gamma \alpha^{(t - 1)}\) to accelerate convergence.

The distribution network could contain multiple adjacent areas besides areas K and L. The proposed DSE is also suitable for other pair of interconnected areas.

By interpreting exchanged information as equivalent pseudo-measurements, the DSE scheme keeps the WLS formulation for each area. As such, for distributed solutions, the bad data detection and identification can be performed the same as integrated solutions. If the measurement redundancy is enough, robust state estimators [8, 34, 35] may be further implemented.

5 Case studies

This section presents test results corresponding to the modified IEEE123-bus system. The data on the IEEE 123-bus system was obtained from [36]. Five DGs are connected to buses 1, 76, 100, 95 and 42, respectively. The control strategies and pseudo-measurements for DGs are shown in Table 1. For DG1, \(r_{\varphi }\) and \(x_{\varphi }\) are set as 0.02 per unit. For DG2-DG5, \(r_{\varphi }\) and \(x_{\varphi }\) are set as 0.02 per unit and 0.2 per unit, respectively. Measurement data with Gaussian noise was generated from the exact power flow results. The maximum percentage measurement errors have been assumed as: 1.5% (bus voltage and branch current magnitude measurements), 3% (power flow measurements) and 50% (pseudo-measurements for loads and DGs connecting to ADNs directly). The virtual measurements for zero injections and pseudo-measurements for DGs connected to ADNs through PWM converters have a very low variance (10−6). For a given maximum error \(e_{zi}\) about the mean value \(\mu_{zi}\), the standard of deviation \(\sigma_{zi}\) of the measurements errors can be computed by

$$\sigma_{zi} = \frac{{\mu_{zi} \times e_{zi} }}{3 \times 100}$$
(27)

The simulation was executed on a 32-bit PC with 1.9-GHz CPU and 4.0-GB RAM in MATLAB environment.

Table 1 Control strategies and pseudo-measurements of DGs
Full size table

5.1 The effectiveness of proposed DG models

To demonstrate the performance of the proposed DG models, errors in SE results by using the proposed method (considering the asymmetric characteristics of DG three-phase outputs) and the conventional method (assuming the phase outputs of DGs in balanced form) are presented in Fig. 4 and Table 2.

Fig. 4
figure 4

DG phase injected power comparison between conventional method and proposed method

Full size image
Table 2 Estimation errors for two methods with respect to true values
Full size table

It can be seen from Fig. 4 and Table 2 that the estimation accuracy by using the proposed method is generally better. Because the modified IEEE 123-bus system operates under unbalanced conditions, the true three-phase outputs of DGs are not in balanced form as shown in Fig. 4. Consequently, the phase-based averaging assumption from the conventional method fails to reveal the unbalanced operating states of DGs, leading to a relatively low estimation accuracy of DG three-phase outputs. Furthermore, the inappropriate DG models used by the conventional method introduce an additional error (or can be understood as corrupted power injection measurements) to the SE calculation, hence the overall estimation accuracy of the whole network states decreases as shown in Table II. In comparison, attributed to the detailed modelling of unbalanced DG power outputs, SE results with a higher quality are available in the proposed method.

Notice that the accuracy of SE results presented in Fig. 4 and Table 2 is acceptable for engineering applications. But it is still possible that high-quality SE results are unavailable considering the limited redundancy of real-time measurements and the pseudo-measurements with low accuracy. In this case, two promising solutions could be taken to enhance the SE performance: ① data-driven state estimation [37], in which informative historical data is further taken advantage of to exploit its connection with the current states, and ② (optimal) placement of PMU units that can effectively increase the SE accuracy (even though the number of PMUs is limited).

5.2 Performance of DSE in a multi-area framework

A set of test systems with an increased number of areas was designed by replicating the modified IEEE 123-bus system to investigate the numerical efficiency of the proposed DSE method. Three different examples are described in Fig. 5:

Fig. 5
figure 5

Diagram of the interconnected multi-area systems by replicating IEEE 123-bus system

Full size image

  • EX1 (four areas): three replicated areas are connected to buses 13, 28 and 64;

  • EX2 (six areas): on the basis of EX1, another two replicated areas are connected buses 21 and 105;

  • EX3 (eight areas): on the basis of EX2, another two replicated areas are connected buses 57 and 135.

Figure 6 presents the computational efficiency comparison between centralized and distributed schemes with respect to EX1-EX3. With the increase of interconnected areas (or bus numbers), the computational burden of the centralized scheme is much heavier than the proposed distributed scheme. This is attributed to the fact that when more areas are replicated, for the distributed scheme, the computational complexity of SE in each area is relatively constant, and only a bit more communication time (or more iteration numbers for local SEs) is needed. But for the centralized scheme, the SE computational complexity is increased with a larger network scale.

Fig. 6
figure 6

Computational efficiency comparison between centralized and distributed scheme with respect to EX1-3

Full size image

On the other hand, numerical stability is another difficult issue faced by SEs at the distribution levels. The numerical stability comparison between the centralized and distributed schemes with respect to EX1-EX3 is depicted in Fig. 7. The condition number of the gain matrix is a key indicator concerning the numerical stability of SE [38]. A relatively high condition number may result in an unstable numerical solution. As seen in Fig. 7, the distributed scheme overshadows the centralized scheme in terms of the numerical stability. As a result of the reduced scale of the SE problem, the numerical stability of the distributed scheme is thereby enhanced.

Fig. 7
figure 7

Numerical stability comparison between centralized and distributed scheme with respect to EX1-3

Full size image

To conclude, the tests regarding computational time and numerical stability corroborate that the computational and numerical efficiency of the proposed DSE algorithm scale are favorable with the interconnected distribution network size.

The stopping criterion was set as 0.001 per unit. Accordingly, for the DSE scheme, three examples reached convergence with iteration numbers being 7, 9 and 12, respectively. Meanwhile, the voltage difference between DSE and ISE was less than 0.1%. Thus, the convergence property and the precision (or optimality) of the augmented Lagrangian-based DSE were generally satisfactory. It is also relevant to clarify that there exists a compromise between precision and computational complexity for DSE. The higher precision of the stopping criterion, the more computational time is needed.

6 Conclusions

A scalable and efficient state estimator that can address the two main challenges (unbalanced modeling of DGs and computational efficiency issues) of ADNSE has been proposed in this paper. A steady-state three-phase DG model considering the unbalanced characteristics of DG three-phase outputs was initially proposed. Subsequently, a feasible strategy to set pseudo-measurements for DGs has been presented. Furthermore, on the premise of extended areas, the augmented Lagrangian-based DSE method was specially designed for multi-area ADNs. As evidenced by the test results, three aspects of advantages for the proposal in this work have been observed: higher accuracy, lower computational effort and superior numerical stability. The proposed DG model attends the first advantage, and the last two are owed to the fully distributed framework. Therefore, this novelty method proposed in our work is a strong stimulus for the smart distribution system implementations.

Emerging future research direction will focus on this work’s application to the ADN operating interdependently with multi-microgrids and the AC-DC hybrid distribution networks (or microgrids).